Der neue Meilenstein der Einheitlichen Wissenschaft ist heute meiner Website zugefügt worden. Die Beschreibung der Bestätigung der Quantisierung des Sonnensystems steht ab sofort hier unten zum Nachlesen bereit.
Es ist die Beschreibung der neusten Entdeckung einer der Konsequenzen der Vereinheitlichung: die direkte Berechnung der globalen energetischen Strahlung der Ur-Sonne. Daraus lernen wir, dass es in der Mitte der Sonne auch heute noch viel wärmer ist, als man es bislang vermutet hat; nämlich etwa 150 Millionen Grad Kelvin. Andererseits ist diese Entdeckung auch ein direkter Beweis, dass das gesamte Universum, auf der kleinen wie auch auf der großen Skala, tatsächlich quantisiert ist. Deswegen anstatt von einem Sonnensystem sollen wir von einem Quanten Sonnensystem sprechen (und denken).
Das Innere der Sonne ist viel heißer als bislang vermutet
(Dies ist der Originalartikel von Peter Jakubowski, veröffentlicht hier am 2 Februar 2022; alle Rechte vorbehalten.)
Die traditionelle Gravitationsphysik und die Einsteinsche Relativitätstheorie beschreiben zwar beide die Dynamik der kosmischen Objekte, aber auf zwei unterschiedlichen Wegen, die miteinander unvereinbar sind. Bislang gibt es für die Allgemeine Relativitätstheorie keine Quantenbeschreibung. Umgekehrt wird auch die Quantenmechanik nur ohne Berücksichtigung der Gravitation formuliert. Und die Newtonsche Gravitationsphysik wurde natürlich auch ohne Quantisierung definiert. Um die aktuelle, ziemlich deprimierende Situation der traditionellen Forschung in der Richtung einer angestrebten Vereinheitlichung zu verdeutlichen, zitiere ich hier zuerst einige Sätze aus dem Forschungsbericht 2016 - Max-Planck-Institut für Gravitationsphysik Quantengravitation und Vereinheitlichung von Nicolai Hermann aus der Abteilung „Quantengravitation und Vereinheitlichte Theorien“.
"Gibt es Hinweise in den experimentellen Daten?
Während Quantenmechanik und ART zur Erklärung beobachteter Phänomene entwickelt wurden (z. B. der Spektrallinien in der Atomphysik), gibt uns die Natur sehr wenige Hinweise, wo wir nach einer Theorie der Quantengravitation schauen sollen. Ein Haupthindernis hier ist, dass die Größenordnung der erwarteten Effekte unglaublich klein ist. Maßgeblich ist die Planck-Länge mit etwa 10−33 cm; entsprechend ist die maßgebliche Skala in Bezug auf die Energie etwa 1019 GeV, unglaubliche 15 Größenordnungen über dem Energiebereich, der für den LHC zugänglich ist. Es besteht daher keine Hoffnung, jemals direkt tatsächliche QG-Effekte im Labor zu messen. Man kann jedoch spekulieren, dass sich QG vielleicht indirekt zeigt, etwa in der kosmischen Hintergrundstrahlung oder dadurch, dass sie eine triftige Erklärung für die Inflation, die dunkle Energie und den Ursprung des Universums liefert. Allerdings muss man sich bewusst sein, dass solche Vorschläge nicht zweifelsfrei zwischen sehr unterschiedlichen Ansätzen unterscheiden können. Beispielsweise, wenn so gegensätzliche Entwürfe wie Stringtheorie und Schleifen-Quantengravitation darum wetteifern, die Eigenschaften des frühen Universums zu erklären. ...
Zusammenfassend kann festgestellt werden: Alle wichtigen Fragen bleiben bislang unbeantwortet, trotz großer Bemühungen und zahlreicher vielversprechender Ideen. ... Es bleibt eine zentrale Herausforderung der Physik, die Struktur der Niederenergiewelt vom Standpunkt einer Planck-Skalentheorie zu erklären."
Die traditionell berechnete Kraft der Gravitation, welche zwischen zwei geladenen Teilchen (z. B., zwischen einem positiv geladenen Proton und einem negativ geladenen Elektron) wirkt, ist viel kleiner als die (auch berechnete) elektromagnetische Kraft zwischen derselben Teilchen. Und der Unterschied ist enorm. Er beträgt 40 Größenordnungen. Dabei muss man wissen, dass 1000 mal kleiner nur 3 Größenordnungen Unterschied bedeutet, und eine Milliarde mal kleiner auch nur 9 Größenordnungen).
Der klassisch berechnete Unterschied zwischen der gravitativen Kraft und der elektromagnetischen Kraft ist also wirklich gewaltig. Aus diesem Grund wurde bislang in der „Quantenwelt“ der elektrisch geladenen Teilchen kaum ihre Gravitation von Bedeutung. In der Welt der kosmischen Körper, auf der anderen Seite, sind die einzelnen elektrischen Ladungen fast immer ganz ausgeglichen (die negativen mit den positiven), so dass eine elektromagnetische Wirkung, zum Beispiel, zwischen der Erde und unserem Mond nie berechnet wird. Stattdessen wirkt sich in diesem Fall nur die Gravitation aus. So die klassische Denkweise.
Die wichtigste Entdeckung der Universalen Philosophie, die auf meiner Einheitlichen Physik basiert, ist die Quantisierung des gesamten Universums. Die einheitliche Beschreibung des Universums muss deshalb nicht nur die Quanteneigenschaften des Lebens, sondern auch eine Art Quantenkosmologie beinhalten, welche die Quantisierung der kosmischen Objekte einschließt. In unserer Einheitlichen Wissenschaft erkennen wir nur eine universelle Wechselwirkung in der gesamten Natur. Das ist der Energietransfer zwischen unterschiedlichen Quanten unseres Universums. Man könnte, rein theoretisch, einen Gradient der übertragenen Energie berechnen, der einer (einheitlichen oder universellen) Kraft gleich wäre. Es wäre aber keine zusätzliche Information damit gewonnen, also lassen wir diese Überlegungen bei Seite. Dafür machen wir aber etwas viel Wichtigeres.
Auf einem früheren Diagramm der Einheitlichen Familie aller möglichen physikalischen Größen habe ich bereits vor einigen Jahren den Zusammenhang der universalen Werte dieser Größen mit den aus der Astrophysik bekannten Werten für das Sonnensystem deutlich gemacht.
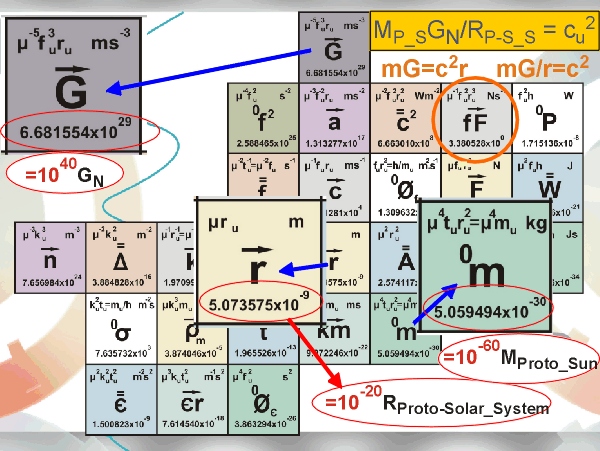
In der rechten oberen Ecke dieses Diagramms sehen wir (auf dem gelben Hintergrund) eine Gleichung, die in der Astrophysik benutzt wird, wenn man die Geschwindigkeiten der einzelnen Planeten, die (im traditionellen Bild) um die Sonne kreisen, berechnen will. Man hat nämlich herausgefunden, dass die Masse der Sonne MS, multipliziert mit der Newtonschen Gravitationskonstante GN, und dividiert durch den Radius RP des Planetenorbits, dem Quadrat der Planeten-Geschwindigkeit (vP) gleicht: MSGN/RP = vP2. In den roten Markierungen unter den hervorgehobenen physikalischen Größen lesen wir, zum Einen, dass der Radius des Ur-Sonnensystems (der vier Ur-Planeten, die die Ur-Sonne begleiteten) um 20 Größenordnungen größer war als der universelle "Radius" eines Quants, ru. Zum Zweiten, dass die Masse der Ur-Sonne um 60 Größenordnungen größer war als die universelle Masse eines Quants, mu. Und zum Dritten, die Newtonsche Gravitationskonstante um 40 Größenordnungen kleiner als die universelle physikalische Größe der Gravitation Gu war (und immer noch ist). Wenn wir also diese Gleichung, wie auf dem Diagramm, für den speziellen Fall des Ur-Sonnensystems (in Englisch: Proto-Solar System) nutzen, bekommen wir als Lösung auf der rechten Seite der Gleichung den Quadrat der universalen Geschwindigkeit cu der Übertragung der Energie im Universum:
(10-60MP-S)x(1040GN)/(10-20RP-SS) = muGu/ru = cu².
Das Innere des Ur-Sonnensystems war also von Anfang an kein Vakuum (im Sinne der Einsteinschen Vakuum-Lichtgeschwindigkeit). Die wichtigste Schlussfolgerung aus dieser Beobachtung kann aber nur eines bedeuten: das Studium der Planetenbewegungen in unserem Sonnensystem offenbart den universalen Quanten Charakter unseres Sonnensystems. Das hat noch niemand vor mir behauptet. Und wahrscheinlich auch nicht mal vermutet.
Wenn das Universum, nicht nur in den kleinsten, sondern auch in den großen Maßstäben quantisiert ist, dann müssen wir jetzt noch den letzten Schritt gehen und uns klar machen, warum alle bisherigen Versuche eine Theorie der Quantengravitation zu formulieren komplett gescheitert sind. Wenn die Masse des Ur-Sonnensystems, die Newtonsche Gravitationskonstante, und die Ausdehnung des Ur-Sonnensystems (bis zum heutigen Asteroiden Gürtel) bekannt sind, und als eine Tatsache in der oberen Gleichung akzeptiert werden müssen, dann müssen wir auch eine andere Variante dieser Gleichung als eine Tatsache akzeptieren:
(10-60MP-S)x(1040GN)x(10-20RP-SS) = 10-40MP-SGNRP-SS = muGuru = Pu,
wo Pu die universale Quantenleistung ist, die aber für alle Quanten des Universums gleich ist (was auf dem Diagramm durch die weiße Hintergrundfarbe dieser Größe betont ist). Konsequent müssen wir aus der oberen Gleichung auch weiter die Information ablesen, dass die gesamte Leistung des Ur-Sonnensystems, PP-S , der Quantenleistung von 1040Quanten gleich war:
PP-S = MP-SGNRP-SS = 1040muGuru = 1040Pu.
Das war eine direkte Folge der Tatsache, dass die Masse der kosmischen "Staubwolke", aus welcher sich das Ur-Sonnensystem geformt hat, hat alle unseren physikalischen Konstanten (die universalen Werte aller physikalischen Größen) auf einmal festgelegt. Einer dieser Werte ist der Wert der universalen Quantenleistung Pu = 17.15136 nW. Das bedeutet, dass die Gesamtleistung des Ur-Sonnensystems 1040x1.715x10-8 W = 1.175x1032 W betragen hat.
Die Größenordnung der Strahlungsleistung der heutigen Sonne (s. Wikipedia) lässt sich aus der Solarkonstanten (E0 = 1361 W/m²) berechnen, weil diese "Konstante" die Strahlungsleistung pro Quadratmeter in der Entfernung der Erde von der Sonne angibt. Das Resultat ist F = 3.828x1026W.
Auch wenn die heutige Sonne nur etwa 40% der Masse der Ur-Sonne hat, und ein Teil der gesamten Leistung von damals auch auf die Planeten berechnet werden muss, muss man nach unserer oberen Berechnung annehmen, dass die Strahlungsleistung der heutigen Sonne, die zum Abschätzen ihrer zentralen Temperatur zu berücksichtigen ist, um etwa 4 Größenordnungen höher ist, als der klassische F-Wert. Nach dem Stefan-Boltzmann Gesetz (s. Wikipedia) bedeutet das, dass die innerste Temperatur der Sonne etwa 10-mal so hoch sein muss, wie bisher angenommen, also etwa 150 Millionen Kelvin betragen muss. Das wird einige Theorien der Energieerzeugung in der Sonne zum Umdenken zwingen. Der zweite Grund dazu ist die dieser Temperatur entsprechende Geschwindigkeit der Energieübertragung (klassisch als Lichtgeschwindigkeit benannte). Sie beträgt dann nämlich nicht die "Einsteinsche" 300 Tausend km/s, sondern 16 Millionen km/s. Diese Tatsachen muss jede Theorie berücksichtigen, wenn sie eine Chance haben soll, uns die Physik der nuklearen Reaktionen im Inneren der Sonne zu erklären.